Two-Way Chi-Square test Using Excel - Statistics Homework Help
You are to determine if there is a significant difference in the following interrogation techniques and whether they produced helpful information.

a) Conduct a chi-square analysis and assume the expected values to be equal. Be sure to state your hypotheses and state your findings in statistical jargon and plain English (1 point).
b) Conduct a chi-square analysis on each technique separately and assume the expected values to be equal. For example, conduct a chi-square analysis for torture vs. information meaningful (yes/no). Do your findings differ among techniques? Be sure to state your hypotheses and state your findings in statistical jargon and plain English (2 points).
|
Solution: (A) We are testing whether the mentioned interrogation techniques produce equally helpful results or not. Formally, the null and alternative hypotheses are:
Ho: All the interrogation methods are equally helpful
Ha: Not all the interrogation methods are equally helpful
The table with the totals for rows and columns is:

Assuming the null hypothesis, the expected percentage of “Yes” is 79.224%. Using that information, we have the following table with the expected values, assuming \({{H}_{0}}\)

We compute now the \({{\chi }^{2}}\) statistics as:
\[{{\chi }^{2}}=\sum{\frac{{{(O-E)}^{2}}}{E}}=44.25427\]We have the critical value \(\chi _{c}^{2}=7.815\) (for 3 degrees of freedom). Since \({{\chi }^{2}}>\chi _{c}^{2}\), we reject the null hypothesis. That means that we have enough evidence to claim that not all the interrogation methods selected are equally useful.
(b) Torture: We have the following hypotheses
\[\begin{array}{cc} & {{H}_{0}}:\text{Positive and negative results for torture are equally likely} \\ & {{H}_{A}}:\text{Positive and negative results for torture are NOT equally likely} \\ \end{array}\]We have the following table
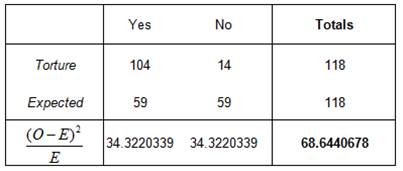
The Chi-Square statistics is equal to \({{\chi }^{2}}=68.6441\), and the critical value is equal to \(\chi_{c}^{2}=3.841\) (for 1 degree of freedom). Therefore, since \({{\chi }^{2}}>\chi _{c}^{2}\), we reject the null hypothesis. That means that we have enough evidence to claim that positive and negative results are not equally useful for “torture”, at the 0.05 level of significance.
Retain/Interview: We have the following hypotheses
\[\begin{array}{cc} & {{H}_{0}}:\text{Positive and negative results for retain/interview are equally likely} \\ & {{H}_{A}}:\text{Positive and negative results for retain/interview are NOT equally likely} \\ \end{array}\]We have the following table
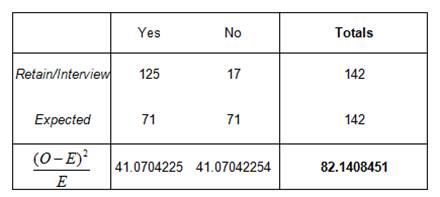
The Chi-Square statistics is equal to \({{\chi }^{2}}=82.1408\), and the critical value is equal to \(\chi _{c}^{2}=3.841\) (for 1 degree of freedom). Therefore, since \({{\chi }^{2}}>\chi _{c}^{2}\), we reject the null hypothesis. That means that we have enough evidence to claim that positive and negative results are not equally useful for “retain/interview”, at the 0.05 level of significance.
Interview: We have the following hypotheses
\[\begin{array}{cc} & {{H}_{0}}:\text{Positive and negative results for interview are equally likely} \\ & {{H}_{A}}:\text{Positive and negative results for interview are NOT equally likely} \\ \end{array}\]We have the following table
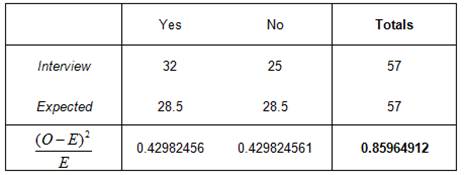
The Chi-Square statistics is equal to \({{\chi }^{2}}=0.8596\), and the critical value is again equal to \(\chi _{c}^{2}=3.841\) (for 1 degree of freedom). Therefore, since is not true that \({{\chi }^{2}}>\chi _{c}^{2}\), we cannot reject the null hypothesis. That means that we don’t have enough evidence to claim that positive and negative results are not equally useful for “interview”, at the 0.05 level of significance.
Hypnosis: We have the following hypotheses
\[\begin{array}{cc} & {{H}_{0}}:\text{Positive and negative results for hypnosis are equally likely} \\ & {{H}_{A}}:\text{Positive and negative results for hypnosis are NOT equally likely} \\ \end{array}\]We have the following table
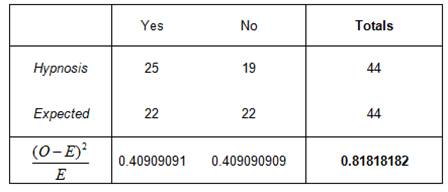
The Chi-Square statistics is equal to \({{\chi }^{2}}=0.81818\), and the critical value is again equal to \(\chi _{c}^{2}=3.841\) (for 1 degree of freedom). Therefore, since is not true that \({{\chi }^{2}}>\chi _{c}^{2}\), we cannot reject the null hypothesis. That means that we don’t have enough evidence to claim that positive and negative results are not equally useful for “hypnosis”, at the 0.05 level of significance.
These conclusions are compatible with what we found in part a).
You can send you Excel Stats homework problems for a Free Quote. We will be back shortly (sometimes within minutes) with our very competitive quote. So, it costs you NOTHING to find out how much would it be to get step-by-step solutions to your Stats homework problems.
Our experts can help YOU with your Statistics Assignments. Get your FREE Quote.
