Using Excel to Work on Correlation and Regression Examples - Statistics HW Help
For parts 1-8, use the data in the table, which shows the personal income and outlays (both in trillions of dollars) for Americans for 11 recent years.
|
Personal Income x |
Personal outlay, y |
|
5.6 |
4.6 |
|
5.8 |
4.9 |
|
6.2 |
5.2 |
|
6.5 |
5.5 |
|
6.9 |
5.8 |
|
7.4 |
6.1 |
|
7.8 |
6.5 |
|
8.4 |
7 |
|
8.7 |
7.3 |
|
8.9 |
7.7 |
|
9.2 |
8 |
Question 1: Construct a scatter plot for the data. Do the data appear to have a positive linear correlation, a negative correlation, or no linear correlation? Explain.
|
Solution: The scatter plot is shown in the figure below:
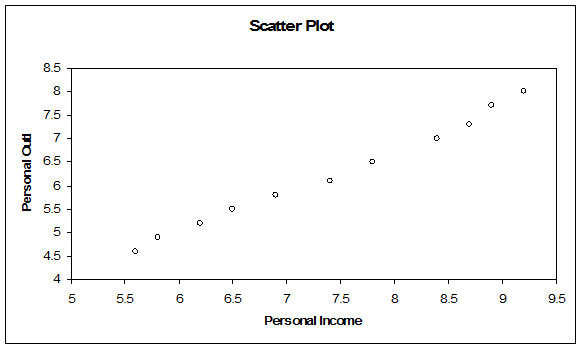
The scatter plot shows a positive correlation. This means that increase in \(x\) is followed by an increase in \(y\).
Question 2: Calculate the correlation coefficient \(r\). What can you conclude?
Solution: Using Excel, we find
|
Personal Income x |
Personal outlay, y | |
|
Personal Income x |
1 |
|
|
Personal outlay, y |
0.995917753 |
1 |
This means that the correlation coefficient is equal to:
\[r=0.9959\]This coefficient is very close to 1, which indicates a very strong (positive) linear association between the variables.
Question 3: Test the level of significance of the correlation coefficient. Use \(\alpha =0.05\)
Solution: We need to test the hypotheses
\[\begin{array}{cc} & {{H}_{0}}:\rho =0 \\ & {{H}_{A}}:\rho \ne 0 \\ \end{array}\]We use a t-test, and the t-statistics is given by:
\[t=r\sqrt{\frac{n-2}{1-{{r}^{2}}}}=0.9959\sqrt{\frac{9}{1-{{0.9959}^{2}}}}=33.0996\]The critical t-value for 9 degrees of freedom and \(\alpha =0.05\) is \({{t}_{c}}=2.262\), which means that we reject he null hypothesis. This means that the correlation is significantly different from zero.
Question 4: Find the equation of the regression line for the data. Include the regression line in the scatter plot.
Solution: We use Excel to find the regression equation. The results are shown in the table below:
|
SUMMARY OUTPUT |
||||||
|
Regression Statistics |
||||||
|
Multiple R |
0.995918 |
|||||
| R Square |
0.991852 |
|||||
|
Adjusted R Square |
0.990947 |
|||||
|
Standard Error |
0.109835 |
|||||
|
Observations |
11 |
|||||
|
ANOVA |
||||||
|
df |
SS |
MS |
F |
Significance F |
||
|
Regression |
1 |
13.21688 |
13.21688 |
1095.589 |
1.03E-10 |
|
|
Residual |
9 |
0.108574 |
0.012064 |
|||
|
Total |
10 |
13.32545 |
||||
|
Coefficients |
Std. Error |
t Stat |
P-value |
Lower 95% |
Upper 95% | |
|
Intercept |
-0.35871 |
0.201982 |
-1.77594 |
0.109475 |
-0.81562 |
0.098207 |
|
Personal Income x |
0.891226 |
0.026926 |
33.09968 |
1.03E-10 |
0.830316 |
0.952136 |
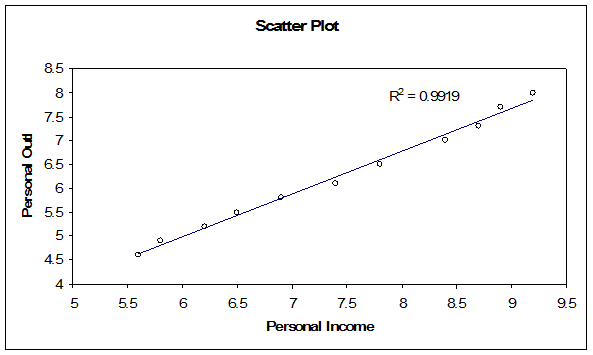
This means that the regression equation is given by
\[\hat{y}=-0.35871+0.891226x \]
The scatter plot with the regression line is shown below:
Question 5: Use the regression line to predict the personal outlays when the personal income is 5.3 trillion dollars.
Solution: We evaluate the regression line at \(x=5.3\) to get
\[\hat{y}=-0.35871+0.891226\times 5.3=4.364789\]which means that predicted personal outlay is $4.364789 trillion dollars
Question 6: Find the coefficient of determination and interpret the results.
Solution: The coefficient of determination is computed as:
\[{{r}^{2}}={{0.995918}^{2}}=0.991852\]This means that 99.1852% of the variation Personal Outlay is explained by Personal Income.
Question 7: Find the standard error of the estimate \({{s}_{e}}\) and interpret the results.
Solution: Using the Excel table above, the standard error is computed as
\[{{s}_{e}}=\sqrt{\frac{\sum{{{\left( {{Y}_{i}}-{{{\hat{Y}}}_{i}} \right)}^{2}}}}{n-2}}=0.109835\]The standard error \({{s}_{e}}\) corresponds to an approximation of the standard deviation of the average response. This standard error is very small, which indicates an excellent linear fit.
Question 8: Construct a 95% prediction interval for personal outlays when personal income is 6.4 trillion dollars. Interpret the results.
Solution: First, the point wise prediction is given by:
\[\hat{y}=-0.35871+0.891226\times 6.4=5.345138\]The 95% prediction interval is given by:
\[CI=\left( \hat{y}-E,\text{ }\hat{y}+E \right)=\left( 5.345138-E,\text{ }5.345138+E \right) \]where
\[E={{t}_{\alpha /2}}\times {{s}_{e}}\sqrt{\frac{1}{n}+\frac{{{\left( X-\bar{X} \right)}^{2}}}{\sum{{{X}^{2}}-n{{{\bar{X}}}^{2}}}}}=2.262159\times 0.109835\sqrt{\frac{1}{11}+\frac{{{\left( 6.4-7.4 \right)}^{2}}}{619-11\times {{7.4}^{2}}}}=0.096552\]which means that
\[CI=\left( 5.345138-E,\text{ }5.345138+E \right)=\left( 5.248586,\text{ }5.44169 \right) \]Question 9: The equation used to predict sunflower yield (in pounds) is
\[\hat{y}=1257-1.34{{x}_{1}}+1.41{{x}_{2}}\]where \({{x}_{1}}\) is the number of acres planted (in thousands) and \({{x}_{2}}\) is the number of acres harvested (in thousands). Use the regression equation to predict the y-values for the given values of the independent variable listed below. Then determine which variable has a greater influence on the value of \(y\)
(a) \({{x}_{1}}=2103,\text{ }{{x}_{2}}=2037\) (b) \({{x}_{1}}=3387,\text{ }{{x}_{2}}=3009\)
(c) \({{x}_{1}}=2185,\text{ }{{x}_{2}}=1980\) (d) \({{x}_{1}}=3485,\text{ }{{x}_{2}}=3404\)
Solution: We have to replace the given values in the multiple regression equation
(a) \(\hat{y}=1257-1.34\times 2103+1.41\times 2037=1311.15\,\text{ pounds}\)
(b) \(\hat{y}=1257-1.34\times 3387+1.41\times 3009=961.11\,\text{ pounds}\)
(c) \(\hat{y}=1257-1.34\times 2185+1.41\times 1980=1120.9\,\text{ pounds}\)
(d) \(\hat{y}=1257-1.34\times 3485+1.41\times 3404=1386.74\,\text{ pounds}\)
The variable that has more (marginal) effect on the absolute value of the response is \({{x}_{2}}\), because its associated regression coefficient is larger in magnitude.
Question 11: A legal researcher is studying the age distribution of juries by comparing them with the overall age distribution of available jurors. The researcher claims that the jury distribution is different from the overall distribution; that is, there is a noticeable age bias in jury selection in this area. The table shows the number of jurors at a county court in one year and the percent of persons residing in that county, by age. Use the population distribution to find the expected juror frequencies. Test the researcher’s claim at \(\alpha =0.01\).
|
21-29 |
30-39 |
40-49 |
50-59 |
60 and above | |
|
Jury |
45 |
128 |
244 |
224 |
359 |
|
Population |
20.50% |
21.70% |
18.10% |
17.30% |
22.40% |
Solution: We need to test the null hypothesis:
\[{{H}_{0}}:{{p}_{1}}=0.205,\text{ }{{p}_{2}}=0.217,\text{ }{{p}_{3}}=0.181,\text{ }{{p}_{4}}=0.173,\text{ }{{p}_{5}}=0.224\]|
21-29 |
30-39 |
40-49 |
50-59 |
60 and above |
Total | |
|
Jury (Observed) |
45 |
128 |
244 |
224 |
359 |
1000 |
|
Expected |
205 |
217 |
181 |
173 |
224 |
1000 |
The Chi-Square statistics is computed as:
\[{{\chi }^{2}}=\sum{\frac{{{\left( {{O}_{i}}-{{E}_{i}} \right)}^{2}}}{{{E}_{i}}}}=279.7048\]The critical value for 4 degrees of freedom, and \(\alpha =0.01\) is
\[\chi _{C}^{2}=13.2767\]Since \({{\chi }^{2}}>\chi _{C}^{2}\), we reject the null hypothesis, which means that the proportions are not the same as in the population.
Question 14: The table shows the age distribution of a random sample of fatally injured male and female passenger vehicle drivers whose blood alcohol content was at least 0.08 in a recent year. Use \(\alpha =0.05\).
|
Gender |
16-20 |
21-30 |
31-40 |
41-50 |
51-60 |
61+ |
|
Male |
155 |
280 |
265 |
225 |
155 |
50 |
|
Female |
60 |
145 |
145 |
130 |
65 |
15 |
Solution: We’ll use a Chi-Square statistics to test for the independence between Gender and Age Group in terms of the number of accidents involving alcohol consumption. We have the following tables:
|
Observed Frequencies | |||||||
|
Age Group |
|||||||
|
Gender |
16-20 |
21-30 |
31-40 |
41-50 |
51-60 |
61+ |
Total |
|
Male |
155 |
280 |
265 |
225 |
155 |
50 |
1130 |
|
Female |
60 |
145 |
145 |
130 |
65 |
15 |
560 |
|
Total |
215 |
425 |
410 |
355 |
220 |
65 |
1690 |
|
Expected Frequencies | |||||||
|
Age Group |
|||||||
|
Gender |
16-20 |
21-30 |
31-40 |
41-50 |
51-60 |
61+ |
Total |
|
Male |
143.7574 |
284.1716 |
274.142 |
237.3669 |
147.1006 |
43.46154 |
1130 |
|
Female |
71.2426 |
140.8284 |
135.858 |
117.6331 |
72.89941 |
21.53846 |
560 |
|
Total |
215 |
425 |
410 |
355 |
220 |
65 |
1690 |
The Chi-Square statistics is computed as:
\[{{\chi }^{2}}=\sum{\frac{{{\left( {{O}_{ij}}-{{E}_{ij}} \right)}^{2}}}{{{E}_{ij}}}}=9.95144\]The critical value for 4 degrees of freedom, and \(\alpha =0.05\) is
\[\chi _{C}^{2}=11.07048\]Since \({{\chi }^{2}}<\chi _{C}^{2}\), we fail to reject the null hypothesis, which means that we don’t have enough evidence to claim that Age Group and Gender are dependent..
In parts 20 and 21, find the critical F-value for a right-tailed test using the indicated level of significance \(\alpha\) and degrees of freedom d.f.N and d.f.D
Question 20: \(\alpha =0.05\), d.f.N = 6, d.f.D = 50
Solution: We have that \({{F}_{C}}=2.286434\)
Question 21: \(\alpha =0.10\), d.f.N = 5, d.f.D = 12
Solution: We have that \({{F}_{C}}=2.394025\)
Question 26: A steel pipe fittings company claims that the yield strength of its nontempered couplings is more variable than that of its tempered couplings. A random sample of nine tempered couplings has a standard deviation of 1.31 megapascals, and a similar sample of nine nontempered couplings has a standard deviation of 25.4 megapascals. From past data, it is known that the company’s production process results in normally distributed yield strengths. Test the company’s claim at \(\alpha =0.05\)
Solution: We need to test
\[\begin{array}{cc} &{{H}_{0}}:{{\sigma }_{1}}={{\sigma }_{2}} \\ &{{H}_{A}}:{{\sigma }_{1}}<{{\sigma }_{2}} \\ \end{array}\]We use an F-test, and the F-statistics is computed as:
\[F=\frac{s_{2}^{2}}{s_{1}^{2}}=\frac{{{25.4}^{2}}}{{{1.31}^{2}}}=375.9455\]The critical value for d.f.N = 8, d.f.D. = 8, \(\alpha =0.05\) is \({{F}_{C}}=3.438103\). Since \(F>{{F}_{C}}\), we reject the null hypothesis, which means that we have enough evidence to support the claim that the yield strength of its nontempered couplings is more variable than that of its tempered couplings, at the 0.05 significance level.
You can send you Excel Stats homework problems for a Free Quote. We will be back shortly (sometimes within minutes) with our very competitive quote. So, it costs you NOTHING to find out how much would it be to get step-by-step solutions to your Stats homework problems.
Our experts can help YOU with your Statistics Assignments. Get your FREE Quote..
