Working of PERT Problems - Operations Management Help

PEARSON CONSTRUCTION CO., INC. (PCCI) - EXERCISE

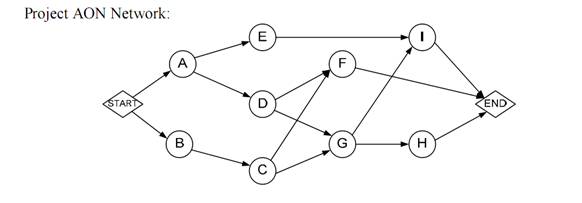
The Pearson Construction Co., Inc. (PCCI) is in the process of building a water tank and installing a pump at one of its construction sites. The following table and project AON network show the information on the activities to be performed and their normal durations (days), as well as the crash durations with their corresponding extra costs'.

Project Information Table:

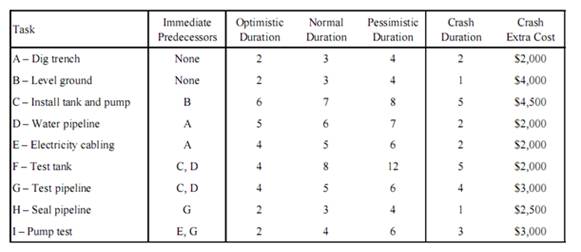
The chief engineer notes that the normal durations specified in the above table are the most likely durations. He also provides the optimistic and pessimistic durations of each of the activities in the table. According to his experience, the task durations follow triangular distributions.

PCCI has promised to deliver the construction in 20 working days. The contract specifies penalties of 2,500 Euros per day late. In addition, the client is interested in getting the construction done as soon as possible, and promises PCCI a bonus of 1,250 Euros for every day of delivery earlier than promised (20 days).

Question I. Based on the current schedule, what is the chance that PCCI will need to pay penalty?

Question 2. Based on the current schedule, what is the chance that PCCI can get extra bonus?

Question 3. If PCCI wants to increase its chance of getting bonuses and/or avoiding penalties, which task should PCCI consider to crash first?

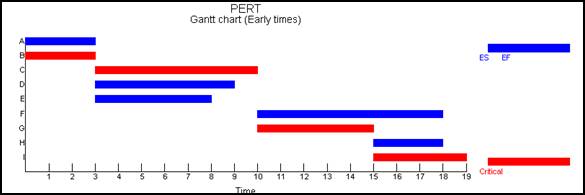
Solution: We have the following chart that summarizes the network information:

We offer quality and prompt Operations Management Homework Help

We can help you with any kind of Operations Management assignments, homeworks, tests, exams, at any level

Including topics such as Forecasting, PERT, Aggregate Planning, Waiting Lines, Network Problems, Linear Programming and Transportation Problems, Inventory, Quality Control and much more.

E-mail your OM Problems for a free quote

Using POM, we get the following results using PERT:

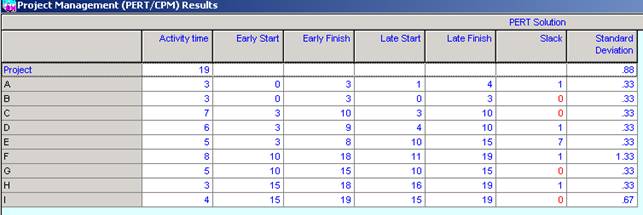
The above table shows that critical activities are B, C, G and I (the activities that cannot be delayed without delaying the completion time). We also have:

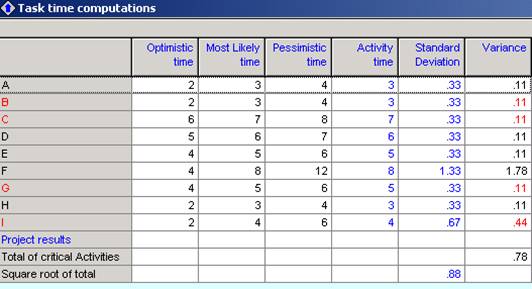
The average completion time is the sum of the average times of the critical path. This means that the average completion time is

\[CT=7+4+5+4=19\text{ days}\]

and the standard deviation is

\[\sigma =0.78\]

1. The probability that the completion time will be above 20 days is

\[\Pr \left( X>20 \right)=\Pr \left( \frac{X-\mu }{\sigma }>\frac{20-\mu }{\sigma } \right)=\Pr \left( \frac{X-19}{0.78}>\frac{20-19}{0.78} \right)=\Pr \left( Z>1.282 \right) \] \[ = 0.0999\]

Now, assuming that PCCI starts accruing penalty if it takes 21 days or more (that is, a penalty for a day late), the probability is

\[\Pr \left( X\ge 21 \right)=\Pr \left( \frac{X-\mu }{\sigma }\ge \frac{21-\mu }{\sigma } \right)=\Pr \left( \frac{X-19}{0.78}\ge \frac{21-19}{0.78} \right)=\Pr \left( Z\ge 2.564 \right) \] \[ =0.005172\]

(Note: If we assume that PCCI starts accruing penalties right after it goes beyond 20 days, i.e., there are penalties for fractions of a day late, then the probability of being fined is the first one, 0.0999)

2. Same as in the previous case, if we assume factional bonus, based on being a faction of a day early, then the probability is

\[\Pr \left( X<20 \right)=\Pr \left( \frac{X-\mu }{\sigma }<\frac{20-\mu }{\sigma } \right)=\Pr \left( \frac{X-19}{0.78}<\frac{20-19}{0.78} \right)=\Pr \left( Z<1.282 \right) \] \[ = 0.9\]

Now, assuming that PCCI starts accruing bonuses only if it gets a reduction in at least one day, the probability is

\[\Pr \left( X\le 19 \right)=\Pr \left( \frac{X-\mu }{\sigma }\ge \frac{19-\mu }{\sigma } \right)=\Pr \left( \frac{X-19}{0.78}\le \frac{19-19}{0.78} \right)=\Pr \left( Z\le 0 \right) \] \[=0.5\]

3. We have the following table with the crashing costs:

Activity	Crash Duration	Cost	Crash Cost / Day
A	2	2,000	1,000
B	1	4,000	4,000
C	5	4,500	900
D	2	2,000	1,000
E	2	2,000	1,000
F	5	2,000	400
G	4	3,000	750
H	1	2,500	2,500
I	3	3,000	1,000

We need to find the critical activity with the cheapest crashing cost / day. Looking at the table, where the critical activities are in boldface, we see that the best alternative to start crashing is G (Test Pipeline).

Medical Imaging Products Corp.

The Medical Imaging Products (MIP) Corp. was anxious to get a new model CATSCAN (computerized axial tomography scanner) onto the market. Past efforts to introduce new models had resulted in frustrating failures. Bret Ricks, president of MIP, was determined that it would not happen again with the newest model. He had no confidence in his current management team, so he hired Jan Dymore, a local consultant, to organize and manage this project. He also assigned an MIP manager, Tom Gort, to work with Jan to start developing some talent for project management within the company. Due to the high uncertainty of the project, Jan decided to take a PERT approach and guided Tom through the process of listing activities, assigning precedence, and estimating completion times. She also explained the critical path concept to Tom, who by this time had a reasonable grasp of the project direction. At the first review meeting with Mr. Ricks, the PERT approach was accepted enthusiastically, but toward the end of the review meeting Jan made some critical remarks about the product design and was subsequently released from the project.

Ricks then asked Tom if he could carry on the PERT approach by himself. Tom jumped at the chance, but later in his office he began to question whether or not he really could use PERT effectively. Jan had made a guess at what the critical path would be and how long the project would take, but she had also told Tom that several other calculations had to be made in order to calculate the time estimates and the variance for each activity. Tom really did not understand the mathematics involved and certainly didn't want to look bad in Rick's eyes, so he decided to take Jan's guess at the critical path and get the best possible estimates of those activity times. By concentrating his attention on the critical path activities and ignoring the variance issues, he is very confident to bring the project in on time.

Question: Will Tom's approach work? What should Tom watch out for?

Solution: No, Tom approach is bound to fail. By ignoring the variance of the activities and concentrating only on the completion times of the activities on the critical path, Tom is only considering the expected value of the project’s completion time. The variance plays a fundamental role, because the actual completion time could be actually quite apart from the expected value, depending on how large is the standard deviation.

It is fundamental to have an accurate estimate of the standard deviation, because that way it would be possible to find a confidence interval for the completion time, which gives a more rounded estimate of what to expect in terms of the actual completion time.

Our experts can help YOU with your Operations Management Homework. Get your FREE Quote. Learn about our satisfaction guaranteed policy: If you're not satisfied, we'll refund you. Please see our terms of service for more information about this policy.