Learn How to Find Optimal Inventory Levels. Operations Management Help
Say you have just had a meeting with John, the Director of Acquisitions. He has been attempting to reduce his costs by placing fewer, but larger, orders for raw materials. You suspect that his department’s actions have been contributing to your organization’s high COS.
Your assignment is to calculate the EOQ/ELS for the following two cases. Include your full calculations:
Raw Material LRM:
Annual demand has historically been about 15,000 units. Each unit costs about $40. For the annual report, due out in June, the corporate accounting department calculates inventory-holding costs by multiplying the value of each item by 0.40. The Director of Purchasing told you that his "cost of ordering" is about $82 per order. He is currently ordering 1,000 at a time. How large should the standard order size be for this product? How much are the Purchasing Director’s policies costing your company? (Calculate the ordering and holding costs associated with his policies and compare them to the "optimal" ordering and holding costs.)
|
Solution: The problem has the following parameters:
Unit Cost = $40
Annual Demand = 15,000
Setup Cost = $82
Holding Cost = $0.40
Based on the assumption of the problem, we can use the EOQ model. We have that
\[{{Q}^{*}}=\sqrt{\frac{2DS}{H}}=\sqrt{\frac{2\times 15,000\times 82}{0.40}}=2,479.919\approx 2,480\]The following table summarizes the situation:
|
Data |
|
| Demand rate, D |
15000 |
| Setup cost, S |
82 |
|
Holding cost, H |
0.4 |
| Unit Price, P |
40 |
|
Daily demand rate |
41.09589041 |
|
Lead time in days |
|
|
Results |
|
|
Optimal Order Quantity, Q* |
2479.919354 |
|
Maximum Inventory |
2479.919354 |
|
Average Inventory |
1239.959677 |
|
Number of Setups |
6.048583789 |
| Holding cost |
$495.98 |
| Setup cost |
$495.98 |
| Unit costs |
$600,000.00 |
|
Total cost, Tc |
$600,991.97 |
| Reorder Point |
0 |
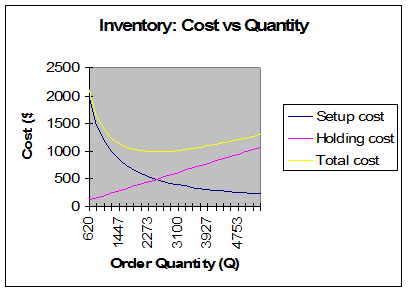
The cost for the optimal quantity \({{Q}^{*}}=2,480\) is computed as (without including the unit costs)
\[TC=\frac{D}{{{Q}^{*}}}S+\frac{{{Q}^{*}}}{2}H=495.98\]The cost for the current ordering size $Q=1,000$is
\[TC=\frac{D}{Q}S+\frac{Q}{2}H=1430\]So, the current policy is costing extra $934.02.
Finished Product CLM:
Annual demand has historically been about 5,700 units. The sales price for each unit of CLM is about $48. The production line that produces CLM can make 100 units per day, but it currently has 170 days per year devoted to manufacturing another project—assume 250 total production days per year. The setup cost for product CLM averages $500 per setup. How large should the production runs be for CLM?
Solution: We have the following table:
|
Inventory |
Production Order Quantity Model |
|
Data |
|
| Demand rate, D |
5700 |
| Setup cost, S |
500 |
|
Holding cost, H |
0.4 |
|
Daily production rate, p |
78 |
|
Daily demand rate, d |
22.8 |
| Unit price, P |
48 |
|
Results |
|
|
Optimal production quantity, Q* |
4487.301 |
|
Maximum Inventory |
3175.628 |
|
Average Inventory |
1587.814 |
|
Number of Setups |
1.270251 |
| Holding cost |
635.1257 |
| Setup cost |
635.1257 |
| Unit costs |
273600 |
|
Total cost, Tc |
274870.3 |
The ELS is computed is equal to \({{Q}^{*}}=\text{4,487}\text{.301}\), and it is computed using the formula
\[{{Q}^{*}}=\sqrt{\frac{2DS}{H\left( 1-\frac{D}{P} \right)}}=\sqrt{\frac{2\times 5,700\times 500}{0.4\left( 1-\frac{5700}{195\times 100} \right)}}=4,487.301\]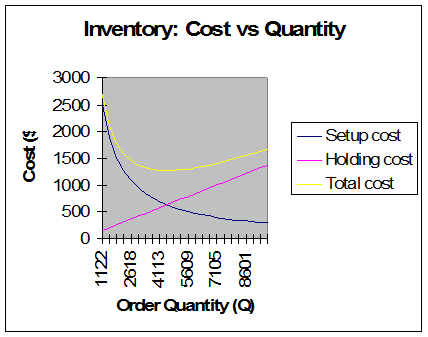
Our experts can help YOU with your Operations Management Homework. Get your FREE Quote. Learn about our satisfaction guaranteed policy: If you're not satisfied, we'll refund you. Please see our terms of service for more information about this policy.
