SPSS Example How to Work on a Correlation Analysis Case Study - SPSS Help

Problem Statement

Certain types of rocket motor are manufactured by bonding together two types of propellant, an igniter and a sustainer. The objective of this study is to analyze the relationship between the strength of this bond and the age of the propellant.

Empirical evidence suggests that this relationship is linear, and the main purpose of this paper is to assess this statement and to find the best possible model, based on a data set of 20 observations from different planes.

The data set obtained is shown below:

Procedures for the Analysis

The first part of the analysis tries to establish the existence of a significant linear relationship between the variables Strength and Age. For this purpose, a scatterplot will be built and the correlation coefficient will be computed. If these procedures indicate that a linear relationship is reasonable, then a full regression model will be computed.

Results Found

First of all, a scatterplot is presented:

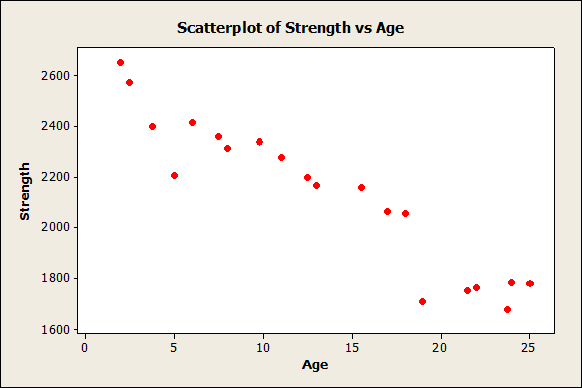
We can observe a clear negative linear trend in the data. It makes sense to apply a linear regression analysis to the data.

The correlation is shown below:

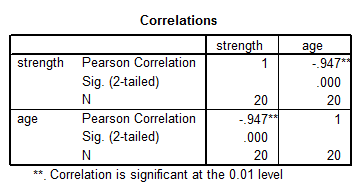
The correlation is R = -0.947, which means that there is a significant degree of negative linear association between Strength and Age. Also from the table, it can be inferred that this correlation is significant at the 0.01 significance level.

The coefficient of determination is

\[{{r}^{2}}={{\left( -\text{0}\text{.9466} \right)}^{2}}=\text{0}\text{.8961}\]

which means that 89.61% of the variation in Strength is explained by Age.

• Now, a linear regression equation is computed. We have the following table:

:

The regression coefficients are computed as

\[b=\frac{n\left( \sum\limits_{i=1}^{n}{{{x}_{i}}{{y}_{i}}} \right)-\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}{n\left( \sum\limits_{i=1}^{n}{x_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)}^{2}}}=\frac{\text{20}\times \text{527613}\text{.638}-\text{266}\text{.75}\times \text{42647}\text{.65}}{\text{20}\times \text{4672}\text{.438}-\text{266}\text{.7}{{\text{5}}^{2}}}=\text{-36}\text{.961}\]

and

\[a=\bar{y}-b\bar{x}=\text{2132}\text{.382}-\left( -\text{36}\text{.961} \right)\times \text{13}\text{.338}=\text{2625}\text{.355}\]

This means that the regression equation is

\[Strength=\text{2625}\text{.355}-\text{36}\text{.961}\,Age\]

The regression table is shown below:

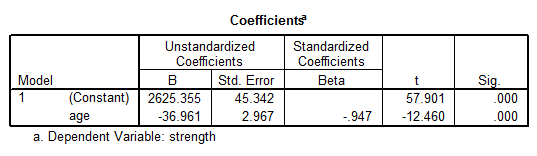
The table above shows that the Age predictor is a significant predictor of the model (\(p = 0.000\)).

• Now, a histogram of residuals is shown:

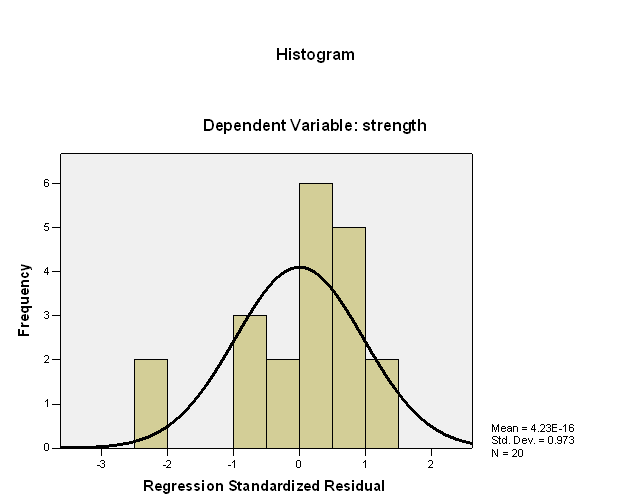
The histogram above shows that the residuals are relatively bell-shaped and there is not a clear violation to the normality assumption.

Finally, we show the plot of residuals versus predicted values:

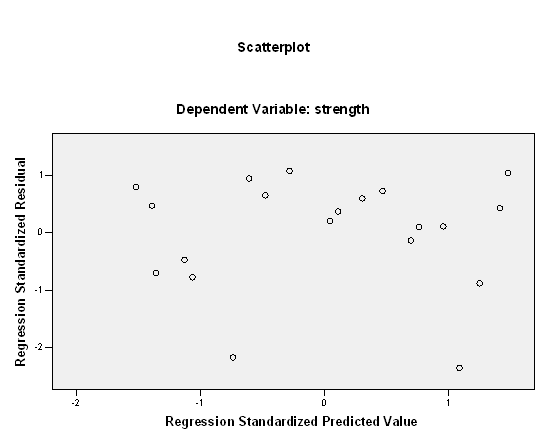
The plot doesn’t show any clear sign of a violation of the homogeneity of variance. Hence, the regression assumptions seem to be satisfied.

Conclusions from the SPSS Regression Results

• A significant correlation was found between the variables Strength and Age. Based on the scatterplot and the correlation, there is a clear negative linear association between them.

• The linear regression equation found is

\[Strength=\text{2625}\text{.355}-\text{36}\text{.961}\,Age\]

• The data don’t seem to violate any regression assumption

References

“Applied Statistics and Probability for Engineers”, D.C. Montgomery, G.C. Runger.

---

You can send you Stats homework problems for a Free Quote. We will be back shortly (sometimes within minutes) with our very competitive quote. So, it costs you NOTHING to find out how much would it be to get step-by-step solutions to your Stats homework problems.

Our experts can help YOU with your Advanced Stats. Get your FREE Quote. Learn about our satisfaction guaranteed policy: If you're not satisfied, we'll refund you. Please see our terms of service for more information about this policy.

Contact Us!