An Example of Using SPSS To Solve a One-Sample Hypothesis Test - SPSS Help
Using attached database of survey responses from the data set, complete the following:
Perform hypothesis testing on one variable’s data. (Choose either the intrinsic or extrinsic column.) Perform a t-test by formulating a null and an alternative statement, choosing an acceptable significance value, selecting the test statistic and determining its value from the sample data, comparing the observed value to the critical value obtained and determining whether to reject or fail to reject the null hypothesis.
In a separate paragraph, provide some information on when to use a t-test and when to use a z-test and why. Also, provide some information about why samples are used instead of populations.
|
We can provide you with the SPSS Help you need, at any level!
Get professional graphs, tables, syntax, and fully completed SPSS projects, with meaningful interpretations and write up, in APA or any format you prefer. Whether it is for a Statistics class, Business Stats class, a Thesis or Dissertation, you'll find what you are looking for with us Our service is convenient and confidential. You will get excellent quality SPSS help for you. Our rate starts at $35/hour. Free quote in hours. Quick turnaround! |
Solution: I choose to test the following hypotheses about Intrinsic Satisfaction:
\[\large \begin{array}{cc} & {{H}_{0}}:{{\mu }_{Intrinsic}}=5 \\ & {{H}_{A}}:{{\mu }_{Intrinsic}}\ne 5 \\ \end{array}\]where \({{\mu }_{Satisfaction}}\) corresponds to the population intrinsic satisfaction. The basic statistics for this problem are shown below:

This means that
\[\large {{\bar{X}}_{Intrinsic}}=5.1440,\text{ }{{s}_{Intrinsic}}=0.99746\]T-test Results from SPSS
We have the following results using SPSS:
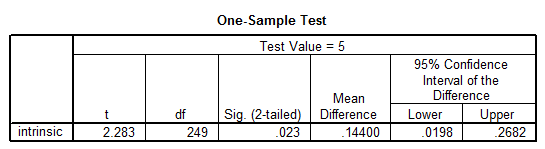
The table above tells us that the value of the t-statistics is
\[\large t = 2.283\]Critical Values
The critical values are \(\pm 1.98\) (if we use normal approximation, the critical values are \(\pm 1.96\). Since the t-statistics is greater in absolute value than 1.96, we reject the null hypothesis. In other words, we have enough evidence to claim that the mean intrinsic satisfaction is different from 5.
Using a different approach, but with an equivalent conclusion we get that the p-value is p = 0.023, which is less than the significance level 0.05, which means that we reject the null hypothesis.
- When to use t-test or z-test: Basically, the z-test is used when the data comes from a normal distribution and the population standard deviation is known. On the other hand, when the data come from a normal distribution, and the sample size is small (\(n < 30\)) and the population standard deviation is not known, then we use a t-test.
Observe that this one-sample approach is only applicable in the case that there is only one-sample, or potentially when you are comparing paired-data.
You can send you SPSS homework problems for a Free Quote. We will be back shortly (sometimes within minutes) with our very competitive quote. So, it costs you NOTHING to find out how much would it be to get help with your SPSS project.
