Check out this One-Way ANOVA Case Study with SPSS
Your grade will be reduced if your solutions are not nicely presented and easy to follow. Be sure that problems are submitted in order. ‘Cut and paste’ relevant computer results into your solutions (do NOT attach them at the end as an appendix). For hypothesis test problems, be sure to start with a statement of the null and alternative hypothesis; show the work involved in reaching a conclusion, and interpret that conclusion in the context of the problem. It’s not enough to say ‘reject H0’. What does that mean?
1. (See included data file)
Suppose that a MBA level stat course is taught using four different methods of instruction: (1) 100% online; (2) a “half and half” format where one week the class meets for a lecture, the next week, material is posted online, etc.; (3) traditional weekly lecture meetings plus supplementary material posted online; and (4) traditional weekly lecture meeting with no use of the web.
Twenty students are surveyed from each course and are asked to estimate the average number of hours per week that they spent on the course, including time spent attending lectures if the course had any. The results appear in the included data file.
(a) Create boxplots for these four sets of data (all on the same graph). Based on the plots, what do you think about the ANOVA assumptions of normal populations and equal variances? (You’ll test these in Part (d), I’m just interested in a visual interpretation here.)
|
We provide SPSS Help for Students, at any level!
Get professional graphs, tables, syntax, and fully completed SPSS projects, with meaningful interpretations and write up, in APA or any format you prefer. Whether it is for a Statistics class, Business Stats class, a Thesis or Dissertation, you'll find what you are looking for with us Our service is convenient and confidential. You will get excellent quality SPSS help for you. Our rate starts at $35/hour. Free quote in hours. Quick turnaround! |
Solution: We have the following box plots:
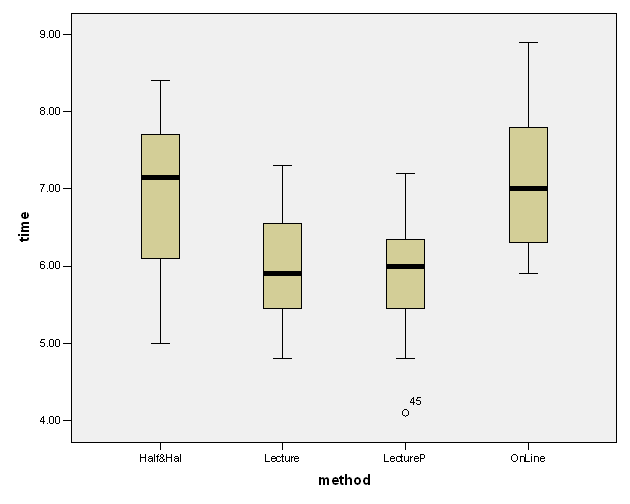
The normality assumption is not completely clear, because the sample distributions are not completely symmetric, but it needs to be determined by a formal normality test.
The homogeneity of variances seems reasonable considering the not too uneven interquartile ranges.
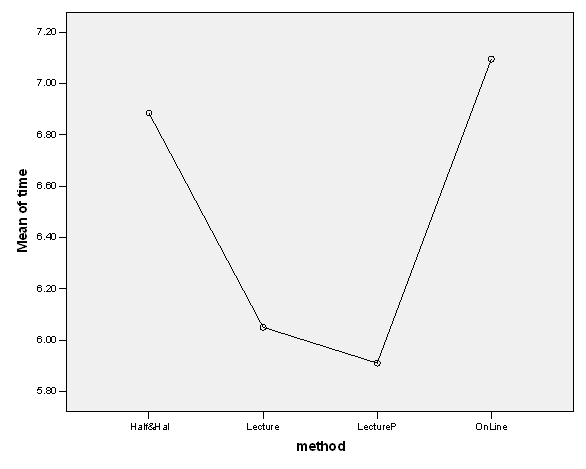
(b) Create interval plots for this data (four intervals on the same plot) so that we can visually compare the four groups. This is the plot that shows a confidence interval for each unknown population mean. Based on the plot, do you believe that the population mean time spent is the same for all groups?
Solution: We have the following interval plots:
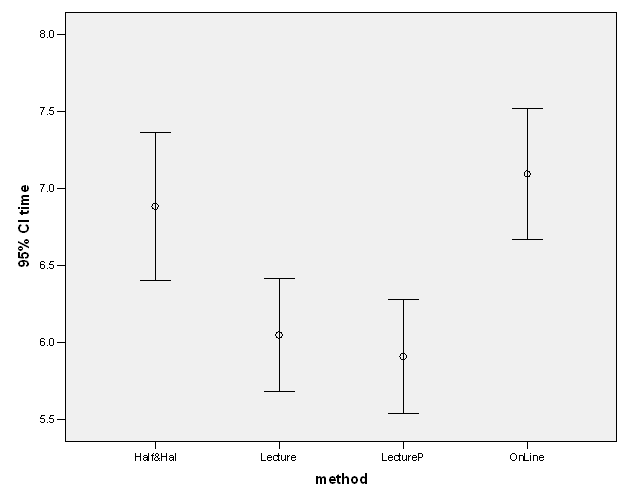
We expect the population means not to be all the same, as several confidence intervals don’t overlap.
(c) Let \(\mu_1\) represent the population mean time spent for method (1), \(\mu_2\) the mean time spent for method (2), and so on. Test the null hypothesis that all means are equal at the 0.05 level of significance.
Solution: Using SPSS we need to test:
\[\begin{array}{cc} & {{H}_{0}}:{{\mu }_{1}}={{\mu }_{2}}={{\mu }_{3}}={{\mu }_{4}} \\ & {{H}_{A}}:\text{ Not all the means are equal} \\ \end{array}\]SPSS ANOVA Results
We get the following results:
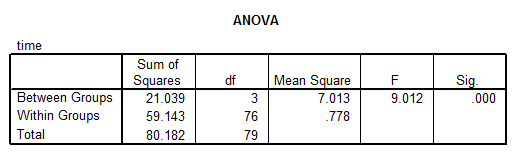
The F-ratio is \(F = 9.012\) and the corresponding p-value is \(p < .001\). This means that we reject the null hypothesis of equal means, at the 0.05 significance level.
(d) Is there evidence of violations of the usual ANOVA assumptions of equal variances and normal populations? Set up and perform appropriate TESTS at the a = 0.05 level of significance.
Solution: We have the following outcome for Levene’s test

The p-value is \(p = .383 > .05\), which means that we fail to reject the null hypothesis of equal variances.
On the other hand, we have the following normality test:
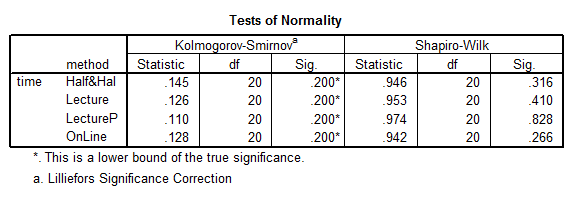
The table above shows that we cannot reject the null hypothesis that all samples come from normal distributions.
(e) If your answer in Part (b) was to “reject H0” then perform an appropriate procedure to determine which means are different from which other means (a visual inspection is not sufficient.).
Post-Hoc Analysis with SPSS
Solution: We have the following Post-Hoc analysis:
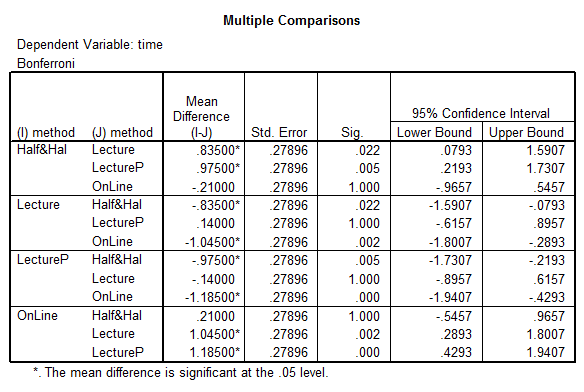
The mean of Online is significantly higher than the rest, except for Half & Half. Also, Half & Half is significantly higher than the rest, except for Online. The means plot is shown below:
Email use your SPSS homework problems for a Free Quote. We will be back shortly (sometimes within minutes) with our very competitive quote. So, it costs you NOTHING to find out how much would it be to get step-by-step solutions to your Stats homework problems.
