A Complete Example of Using Minitab to Work on Several T-test Problems - Minitab Help

1. The provided data arrows2samp.txt gives efficiency measurements (in terms of the

actual kinetic energy in the launched arrow as a percentage of its potential energy) on two types of arrow shafts (types coded as 2213 and 2117) measured 20 meters downrange from the launching bow. The experiment was conducted as follows: Since there may be “archer” effects, 20 male subjects were randomly selected from a pool of candidates to serve as archers. Each archer launched an arrow shaft of each type, using a coin flip to determine order. All 40 of these measurements were carried out in completely random order.

a. Discuss the assumptions of the procedure you intend to use to compare the mean efficiency of shaft type 2213 to shaft type 2117.

Solution: Basically, we have to compare two paired samples with unknown population and low sample size, which means that the appropriate test would be the t-test for paired samples. Nevertheless, there are certain assumptions that must be satisfied. One of those is the normality of the data, or at least non severe violation of normality.

Results From Minitab

Using Minitab, we apply the Anderson-Darling normality test. The following is the outcome:

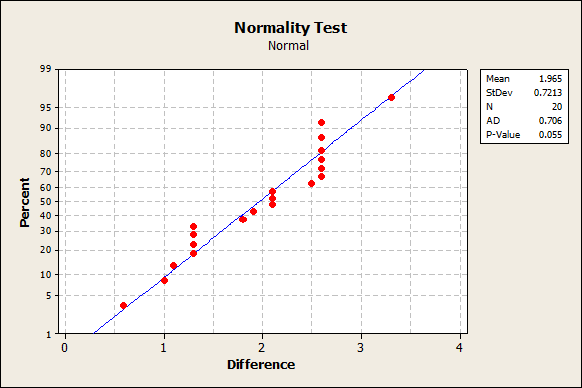
We notice that the p-value is 0.055, which implies it’s not significant (greater than 0.05), and therefore we have normality at the \(\alpha =0.05\) significance level.

Our hypotheses are:

\[\begin{array}{cc} & {{H}_{0}}:\text{There }\!\!'\!\!\text{ s no difference in the efficiency} \\ & {{H}_{1}}:\text{There }\!\!'\!\!\text{ s a difference in the efficiency} \\ \end{array}\]

Now, we apply the t-test for paired samples using Minitab. The following is the outcome

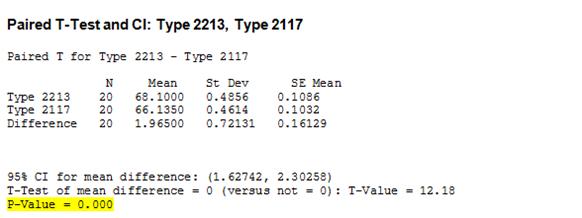
The p-value is 0.000, and thus it means that we reject the null hypothesis, which means that shaft type 2213 to shaft type 2117 have different efficiencies, at the 0.05 level of significance.

b. Construct and interpret a 95% confidence interval for the difference in (long-run) mean efficiencies between the two shaft types.

Solution: As we saw in the previous part, with the help of MINITAB we compute the following output:

That means the 95% CI for the mean difference is

\[CI = (1.62742,\text{ 2}\text{.30258)}\]

The interpretation of this interval is that there’s a 95% chance that this interval will contain the actual difference between the two population means.

2. An experimenter set up a simulated manufacturing line consisting of a team of subjects whose job it was to construct a fairly complex dinosaur out of Lego blocks. Each team was allowed an hour to construct as many such dinos as it could, and after that time the response

Y = proportion of acceptable dinos constructed

was recorded for the team. This process was repeated for 28 teams. Fourteen of the teams had their quality inspected by a “foreman”, whereas the other fourteen teams were held responsible for their own quality. In all other respects, the teams were given identical instructions, and the 28 experimental runs were done in completely random order. The provided data dinos2.txt has two variables; the first represents the values of Y for the “foreman-based” quality control approach, the second for the “worker-based” approach.

a. Conduct a test of the hypothesis of homoskedasticity. Give hypotheses, a P-value, and an interpretation. Do you feel comfortable doing this test for this data? Why or why not?

Solution: We call \(\sigma _{F}^{2}\) to the population variance of the foreman-based group, and \(\sigma _{W}^{2}\) to the population variance of the worker-based group. Our hypotheses are

\[\begin{array}{cc} & {{H}_{0}}:\sigma _{F}^{2}=\sigma _{W}^{2} \\ & {{H}_{A}}:\sigma _{F}^{2}\ne \sigma _{W}^{2} \\ \end{array}\]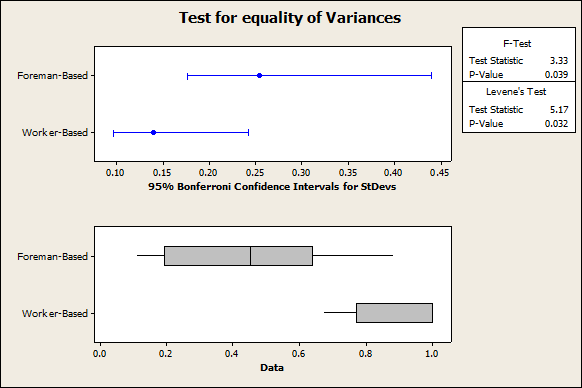

Results From Levene's Test Using Minitab

Using Levene’s test for homogeneity of variances we get a p-value of 0.032, which is not significant. That means that we reject the null hypothesis and we can say that the variances are unequal at the 0.05 level of significance. Levene’s test is more frequently used to check the homoskedasticity of a group of several variables. But the p-value for the F test (comparison between 2 variances) is also significant, and thus compatible with Levene’s test.

b. What test would you use for the hypothesis that the long-run mean proportion of acceptable dinos constructed under the foreman-based approach does not differ from that of the worker-based approach? Justify your answer; in doing this, say (for example) which diagnostics you inspected and interpret each of these.

Solution: We should use t-test for 2 samples, under the assumption of unequal variances because the population variance is unknown and sample size is small (less than 30). We need to check fist the normality of the data. We are going to use Minitab to apply the Anderson-Darling normality test to both foreman-based and worker-based

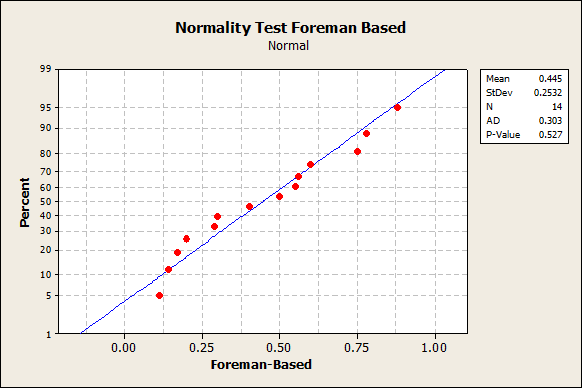
This is the Anderson-Darling normality test. We see that the p-value is 0.527, which is not significant (because is less than 0.05, the given level of significance). Therefore, we can assume normality in the foreman-based group.

Now, we apply the Anderson-Darling normality test to the other group. The output is the following:

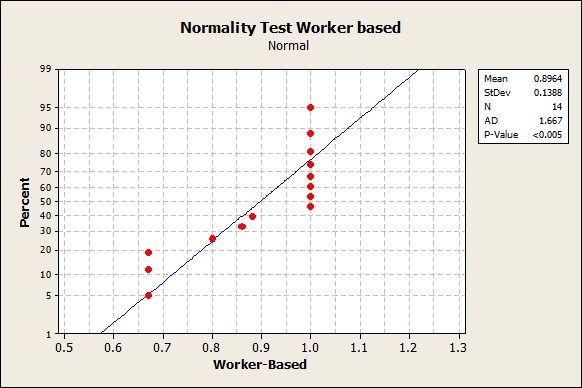
the p-value is 0.005, which means that it’s significant and we reject normality. Nevertheless, if we apply Ryan-Joiner we get

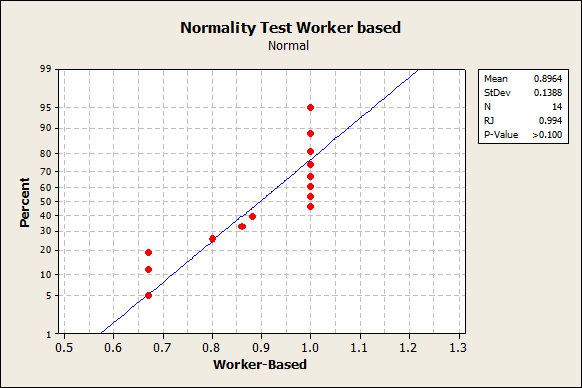
and since the p-value is 0.1, the result is not significant. There’s a contingency in the results of these test. Normally t-test would work even though the normality is not totally satisfied. We still expect a reasonable normal approximation given the contingency found in the outcome of the two tests for normality.

c. Conduct the test referred to in art (b); provide hypotheses, test statistic value, P-value and interpretation.

Solution: We call \({{p}_{F}}\) to the population proportion of the foreman-based group, and \({{p}_{W}}\) to the population proportion of the worker-based group. Our hypotheses are

\[\begin{array}{cc} & {{H}_{0}}:{{p}_{F}}={{p}_{W}} \\ & {{H}_{A}}:{{p}_{F}}\ne {{p}_{W}} \\ \end{array}\]

We get the following result with Minitab:

The p-value is 0.000, which means it’s significant. Therefore, we can reject the null hypothesis of equality of means, which means that the long-run mean proportion of acceptable dinos constructed under the foreman-based approach does differ from that of the worker-based approach, at the 0,05 level of significance

d. Construct and interpret a 90% confidence interval for the difference in long-run means between the two strategies.

Solution: Using Minitab again we obtain the following table:

That means the 90% CI for the mean difference is

\[CI = (-0.584551,\text{ -0}\text{.318306)}\]

---

Do you have any Minitab questions? Send us your Minitab problems for a Free Quote. We will be back shortly with our very competitive quote. So, it costs you NOTHING to find out how much would it be to get step-by-step solutions to your Stats homework problems.

Contact Us!