Regression Model Building: A Case Study Using SPSS

Multiple Regression Analysis of Brain Size and Intelligence

Number of cases: 40

Variable Names:

1. Gender: Male or Female (Male = 1 and Female = 2)
2. FSIQ: Full Scale IQ scores based on the four Wechsler (1981) subtests
3. Intelligence Level (1= Below Average, 2 = Average and 3= Above Average).
4. VIQ: Verbal IQ scores based on the four Wechsler (1981) subtests
5. PIQ: Performance IQ scores based on the four Wechsler (1981) subtests
6. Weight: body weight in pounds
7. Height: height in inches
8. MRI Count: total pixel Count from the 18 MRI scans (in units of thousands, for example a value of 817 would be equivalent to 817 thousand).

The information above describes the dataset "Brain Size and Intelligence". You are to use SPSS to answer analyze the Brian Size and Intelligence" data file to answer the following questions.

Include the following for each answer:

A. The rationale or justification for your analysis

B. An interpretation of your results.

C. Include your SPSS outputs

D. Please make sure to use all the statistical results terminology (e.g. t = 3.45, p = .000; r = .75, p = .000; X²(2) = 7.89, p = .000) when reporting your results.

1. Describe the relationship between height and weight. Interpret this result.

Solution: The first thing to do is to graph height versus weight. We get the following SPPS output:

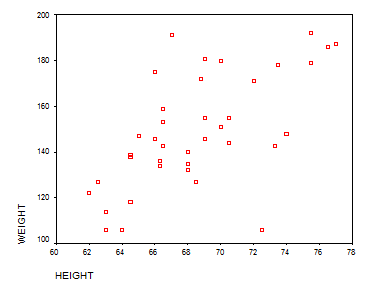
The points are a little bit spread out, but taking some outliers aside we can see a positive correlation between the variables. We’ll apply a linear regression now. We get the following SPSS output:

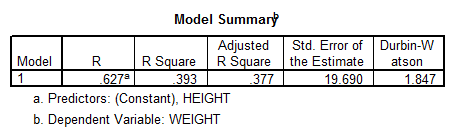
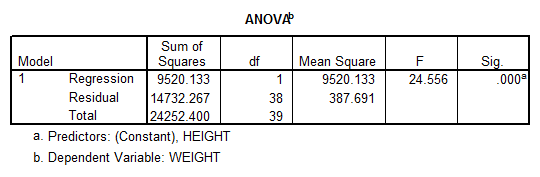
Interpretation of the Results: The correlation coefficient \(R=0.627\) is significant (according to the critical value of the Pearson Correlation coefficient, for \(n=40\), indicating a degree of linear association between height and weight.

Nevertheless, the coefficient \({{R}^{2}}=0.393\) indicates that only 39.3% of the variance is explained by the linear regression, therefore the linear association is rather weak.

Moreover, the ANOVA results indicate that the model is significant, which means that the independent variables do a good job explaining the variation in the dependent variable. The linear model we use, with caution, is:

\[Weight=-117.917+3.899\times Height\]

2. Describe the relationship between FSIQ and Weight. Interpret what this result means.

Solution: Again, the first thing to do is to graph height versus weight. We get the following SPPS output:

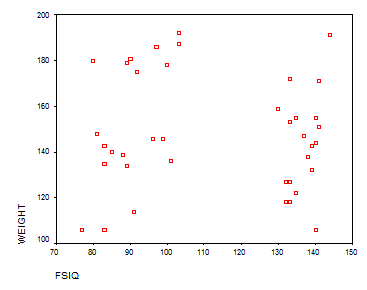
Here we see a totally scattered graph, with no apparent relationship between FSIQ and Weight. We’ll run a regression to confirm our appreciation:

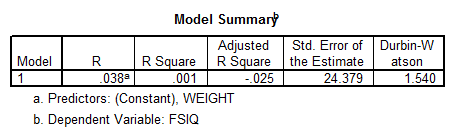
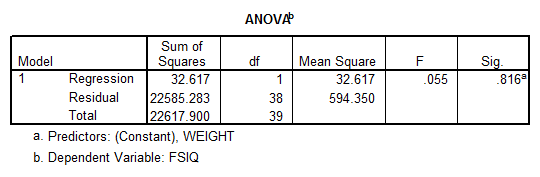
Interpretation of the Results: There’s not a significant linear relationship between WEIGHT and FSIQ. Also the ANOVA table shows that the p-value is significant, which means that the independent variable WEIGHT doesn’t explain appropriately the independent variable FSIQ.

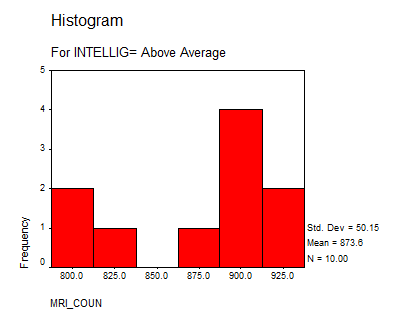
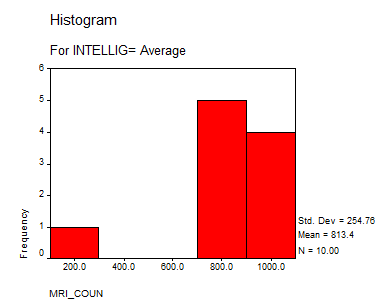
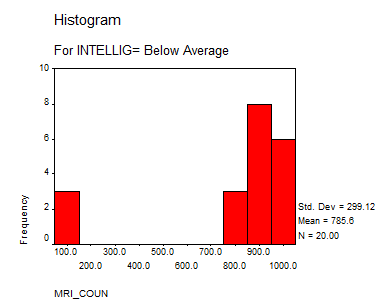
3. What is the mean MRI count for below average, average and above average psychology students?

Solution: We use the “Explore” option to get

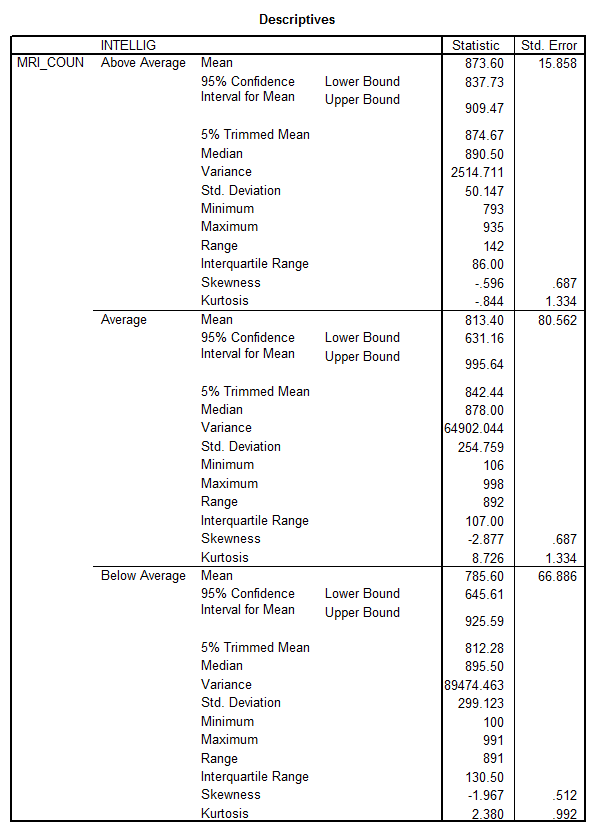
Summarizing:

4. Produce a histogram of the MRI counts for each of the three intelligence level categories

Solution: We present the following histograms:

a. Does the data meet the assumptions of homogeneity of variances (similar variances among groups) and normality necessary for conducting parametric data analysis procedures?

Solution: We apply Levene’s Test to check homogeneity of variances:

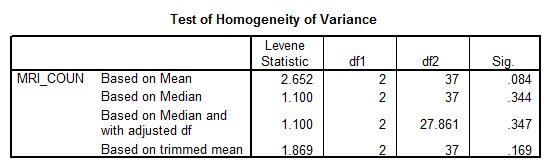
Interpretation of the Results: Since all the p-values are greater than 0.05, we can assume homogeneity of variances.

For normality, we apply Shapiro-Wilk test:

Interpretation of the Results: We can say that the group “Above Average” doesn’t differ significantly from a normal distribution, but the “Average” and “Below Average” do. This suggests that we may need to increase the size sample or to reduce bias on the sampling process.

b. Is there a significant difference between mean MRI counts for students classified in the three intelligence level categories referred to question #3? Interpret the results from the analysis that you would use to answer this question.

Solution: We are going to perform an ANOVA analysis. The analysis should be performed with caution due to the lack of normality of some of the groups.

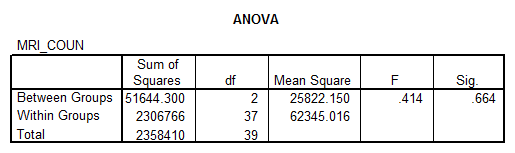
Interpretation of the Results: The p-value is 0.664 which is not significant. Therefore, we cannot reject the null hypothesis of equal means. But we have to be a little suspicious about this result due to the lack of normality of some of the groups.

What Makes Kids Popular

The participants for this study were students in grades 4-6 from three school districts in Ingham and Clinton Counties, Michigan. Chase and Dummer stratified their sample, selecting students from urban, suburban, and rural school districts with approximately 1/3 of their sample coming from each district. Students indicated whether good grades, athletic ability, or popularity was most important to them. They also ranked four factors: grades, sports, looks, and money, in order of their importance for popularity. The questionnaire also asked for gender, grade level, and other demographic information.

Number of cases: 478

Variable Names (Please refer to your SPSS data file, "What Makes Kids Popular").

1. Gender: ( Boy = 1 or Girl = 2)

2. Grade: 4th, 5th or 6th

3. Age: Age in years

4. Urban/Rural ( Rural =1, Suburban=2, or Urban school district=3)

5. Goals: Student's choice in the personal goals question where options were 1 = Make Good Grades, 2 = Be Popular, 3 = Be Good in Sports

6. Grades: Rank of "make good grades" (1=most important for popularity, 4=least important)

7. Sports: Rank of "being good at sports" (1=most important for popularity, 4=least important)

8. Looks: Rank of "being handsome or pretty" (1=most important for popularity, 4=least important)

9. Money: Rank of "having lots of money" (1=most important for popularity, 4=least important) )

Reference: Chase, M. A., and Dummer, G. M. (1992), "The Role of Sports as a Social Determinant for Children," Research Quarterly for Exercise and Sport, 63, 418-424.

The information above describes the dataset "What Makes Kids Popular". You are to use SPSS to answer analyze the popular kids data file to answer the following questions.

Include the following for each answer:

A. The rationale or justification for your analysis

B. An interpretation of your results.

C. Please make sure to use all the statistical results terminology (e.g. t = 3.45, p = .000; r = .75, p = .000; X²(2) = 7.89, p = .000) when reporting your results.

1. What was the percent of students were from rural, suburban and urban schools?

Solution: Let’s use SPSS to address this question:

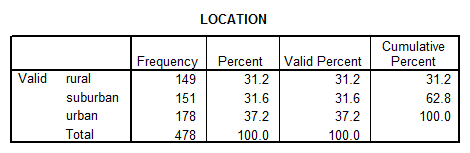
2. What percent of students felt that Grades where the most important goal for them?

Solution: Again, let’s use SPSS to address this question:

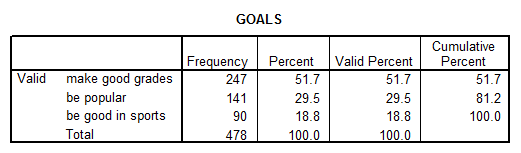
This means that 51.7% of students felt that Grades where the most important goal for them.

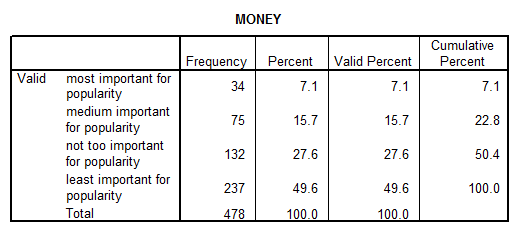
3. What was the frequency of responses (ranging from 1 to 4) to the question that asked students to rate importance of being popular in relation to "having lots of money"?

Solution: Using SPSS we get:

4. Is there significant a relationship between gender and the type of personal goals (variable #5) that students indicated where important to them? How do you know? Interpret the results from that analysis that you would conduct to answer this question.

Solution: Using SPSS we get the following cross tab:

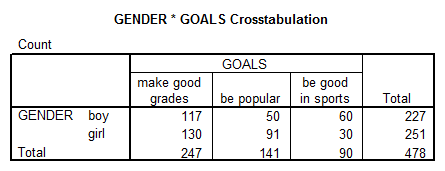
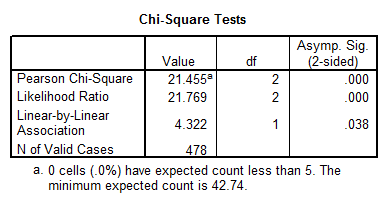
Interpretation of the Results: The p-value equal to 0.000 indicates a relationship between GENDER and GOALS.

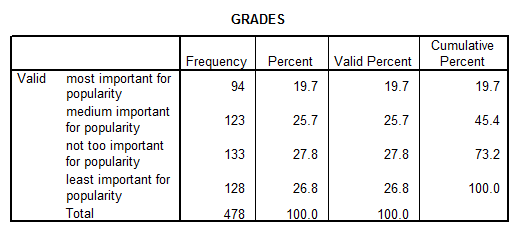
5. A. Describe how students ranked responses for the question "Making Good Grades".

Solution: We get the following SPSS output

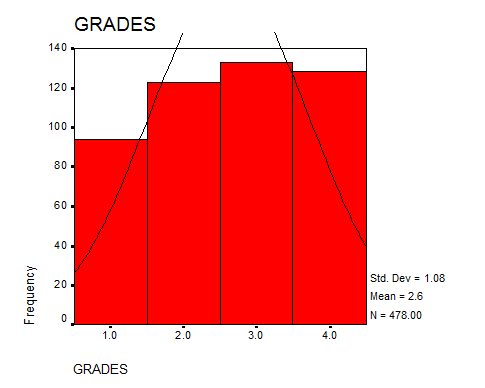
B. Did the boys average ranking for this question differ from that of the girls?

Solution: We have that

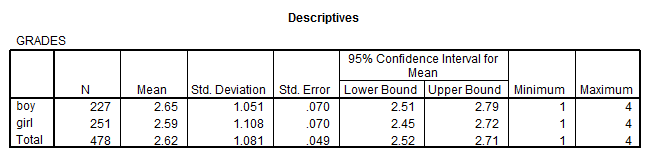
This means that the boys average ranking for this question differ from that of the girls.

C. Was the difference significant? Interpret the results from the analysis that you would conduct to answer this question.

Solution: We perform an ANOVA to get:

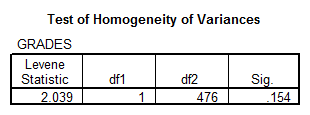
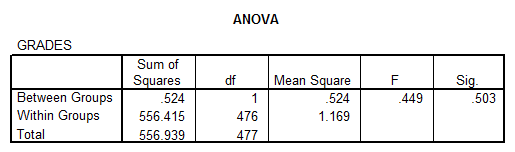
Interpretation of the Results: We can assume homogeneity of variances according to the results of the Levene’s test, and the ANOVA table shows a p-value of 0.503, which indicate that the difference between the means is not significant.

6. For questions 4 and 5, what does it mean when we make the decision that a result is significant? Be sure to address the issues of:

a. Probability

b. Type I errors (Alpha)

c. Type II errors (Beta)

Make sure that you explain these concepts using the results you obtained from questions 5 and 6.

Solution: A result is significant when the value of the associated statistic indicates that we have to reject the null hypothesis, or equivalently, that the p-value is less than the significance level. This means that under the assumption that the null hypothesis is true, and then the result of the statistic is an “abnormal” one. That means that under the assumption that the null hypothesis is true, the probability of rejecting the null hypothesis (Type I error) is \(1-\alpha\), where \(\alpha\) is the significance level. Normally, the tests make sure that the error of type I is controlled (by \(\alpha\)), but they don’t control the type II error (which the probability of accepting the null hypothesis when it’s false). As a matter of fact, there’s a compromise between \(\alpha\) and \(\beta\), meaning that we cannot make them arbitrarily small at the same time.

---

You can send you Stats homework problems for a Free Quote. We will be back shortly (sometimes within minutes) with our very competitive quote. So, it costs you NOTHING to find out how much would it be to get step-by-step solutions to your Stats homework problems.

Our experts can help YOU with your Stats. Get your FREE Quote. Learn about our satisfaction guaranteed policy: If you're not satisfied, we'll refund you. Please see our terms of service for more information about this policy.

Contact Us!